《Unity着色器圣经》4.1.1. | Sin and Cos function.

目录索引

译文

这些三角函数指的是角度的正弦和余弦，即：

余弦是指，相邻边和斜边之间的比率。

正弦是指，对边和斜边之间的比率。

其语法如下：

float cos (float n);
float2 cos (float2 n);
float3 cos (float3 n);
float4 cos (float4 n);

float sin (float n);
float2 sin (float2 n);
float3 sin (float3 n);
float4 sin (float4 n);

标量值和向量上都可以使用“cos和sin”。

这些函数也包含在Cg/HLSL语言中，在计算机图形学中非常有用。有了它们，我们可以生成多个几何图形，甚至矩阵变换。实现的一个实际示例是对象中顶点的旋转。

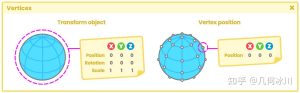
正如我们已经知道的，一个顶点有三个空间坐标（XYZ）作为向量。考虑到它的性质，我们可以变换这些值，并从矩阵中产生旋转的感觉。

让我们想象一下，我们想要在二维空间中旋转一个顶点。在其“Y”轴上应用函数“sin”将获得从上到下的变动。在其“X”轴上使用函数“cos”将再现圆形运动。

为了理解这个概念，我们将执行以下操作：我们将创建一个新的着色器类型“Unlit shader”，我们将其称为USB_function_SINCOS。我们将使用此着色器在立方体的顶点上生成一个小的旋转动画。我们将首先声明一个有范围的float变量，稍后我们将在函数中使用该范围来确定转速。

Shader "USB/USB_function_SINCOS"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _Speed ("Rotation Speed", Range(0, 3)) = 1
    }
    SubShader { ... }
}

我们需要矩阵的帮助来旋转坐标；在第3.2.7节中我们提到过矩阵，忘记的小伙伴可以去复习一下。这一次，我们将在我们的物体上使用一个3X3矩阵（float3x3）。

Pass
{
   ...
    sampler2D _MainTex;
    float4 _MainTex_ST;
    float _Speed;

    // let's add our rotation function
    float3 rotation(float3 vertex)
    {
        // create a three - dimensional matrix
        float3x3 m = float3x3
        (
            1, 0, 0,
            0, 1, 0,
            0, 0, 1
        );
        // let’s multiply the matrix times the vertex input
        return mul(m, vertex);
    }
   ...
}

“旋转”函数返回一个三维向量，它不执行任何特定的操作，因为矩阵“m”只有它的特定的值。但是，我们可以稍后在顶点着色器阶段使用它来变换对象的顶点。

我们将从选择旋转轴开始；我们将注意下图。

在上图中，每个矩阵表示一个旋转变换轴。举个例子，在这里，我们将使用“Y”轴（RY轴）进行演示。因此，我们将在旋转方法中添加两个float变量，使用sin和cos三角函数。

float3 rotation(float3 vertex)
{
    // let’s add the rotation variables
    float c = cos(_Time.y * _Speed);
    float s = sin(_Time.y * _Speed);

    // create a three - dimensional matrix
    float3x3 m = float3x3
    (
        c, 0, s,
        0, 1, 0,
        -s, 0, c
    );
    // let’s multiply the matrix times the vertex input
    return mul(m, vertex);
}

稍后，在4.2.4节中，我们将详细讨论“_Time”属性。现在，我们只考虑这个变量将时间添加到操作中，与C#中的Time.timeSinceLevelLoad的行为非常相似。

_Time会影响场景中立方体的顶点，因此它们将开始根据旋转轴移动。

为了让旋转功能可以完美运行，我们必须在顶点着色器阶段实现它。为此，我们必须考虑UnityObjectToClipPos方法，因为如第3.3.2节所述，它允许将对象的顶点从对象空间转换到剪辑空间。因此，在将顶点的坐标转换为屏幕位置之前，我们必须实现顶点的旋转。

v2f vert (appdata v)
{
    v2f o;
    float3 rotVertex = rotation(v.vertex);
    o.vertex = UnityObjectToClipPos(rotVertex);
    o.uv = TRANSFORM_TEX(v.uv, _MainTex);
    return o;
}

在这个例子中，我们已经声明了一个名为“rotVertex”的新三维向量。其中存储了网格顶点的输入及其在对象空间中的旋转。然后，该向量被用作UnityObjectToClipPos方法中的参数。

如果我们回到Unity并按下Play按钮，我们将看到所有立方体顶点作为一个整体在旋转。

---

原文对照

These trigonometric functions refer to the sine and cosine of an angle, that is:

• The ratio between the adjacent leg and the hypotenuse, in the case of cosine.
• And the ratio between the opposite leg and the hypotenuse, in the case of sine.
  Its syntax is as follows:

float cos (float n);
float2 cos (float2 n);
float3 cos (float3 n);
float4 cos (float4 n);

float sin (float n);
float2 sin (float2 n);
float3 sin (float3 n);
float4 sin (float4 n);

We can use both “cos and sin” on scalar values and vectors.

These functions also included in the Cg/HLSL language are very useful in Computer Graphics. With them, we can generate multiple geometric figures and even matrix transformations. A practical example of implementation is the rotation of vertices in an object.
As we already know, a vertex has three space coordinates (XYZ) considered as vectors. Given its nature, we can transform these values and generate the illusion of rotation from a matrix.
Let’s imagine that we want to rotate a vertex in a two-dimensional space. Applying the function “sin” on its “Y” axis will obtain a wave motion going from top to bottom. Using the function “cos” on its “X” axis will reproduce a circular motion.

To understand the concept, we will do the following: we will create a new shader type, “Unlit Shader,” which we will call USB_function_SINCOS. We will use this shader to generate a small rotation animation on the Cube’s vertices. We will start by declaring a floating range, which we will use later in the function to determine the rotation speed.

Shader "USB/USB_function_SINCOS"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _Speed ("Rotation Speed", Range(0, 3)) = 1
    }
    SubShader { ... }
}

We need the help of a matrix to rotate coordinates; in section 3.2.7, we were able to review its structure using matrices of different dimensions. This time, we will use a three times three- dimensional matrix (float3x3) on our object.

Pass
{
   ...
    sampler2D _MainTex;
    float4 _MainTex_ST;
    float _Speed;

    // let's add our rotation function
    float3 rotation(float3 vertex)
    {
        // create a three - dimensional matrix
        float3x3 m = float3x3
        (
            1, 0, 0,
            0, 1, 0,
            0, 0, 1
        );
        // let’s multiply the matrix times the vertex input
        return mul(m, vertex);
    }
   ...
}

The “rotation” function returns a three-dimensional vector, and it does not perform any specific action because the matrix “m” has only its identity values. However, we can use it later to transform the vertices of an object in the vertex shader stage.

We will start by selecting a rotation axis; we will pay attention to the following diagram.

In the figure above, each of the matrices represents a rotation transformation axis. To exemplify, in this opportunity, we will perform the exercise using the “Y” axis (RY axis). Therefore, we will have to add two floating variables in the rotation method, using sin and cos trigonometric functions.

float3 rotation(float3 vertex)
{
    // let’s add the rotation variables
    float c = cos(_Time.y * _Speed);
    float s = sin(_Time.y * _Speed);

    // create a three - dimensional matrix
    float3x3 m = float3x3
    (
        c, 0, s,
        0, 1, 0,
        -s, 0, c
    );
    // let’s multiply the matrix times the vertex input
    return mul(m, vertex);
}

Later, in section 4.2.4, we will talk about the “_Time” property in detail. For now, we will only consider that this variable adds time to the operation, very similar to the behavior of Time. timeSinceLevelLoad in C#.

_Time will influence the Cube’s vertices in our scene, so they will start to move according to their rotation axis.

The rotation function can operate perfectly; now, we must implement it on the vertex shader stage. For this purpose, we must consider the UnityObjectToClipPos method since, as explained in section 3.3.2, it allows transforming the vertices of an object from object- space to clip-space. Therefore, we will have to implement the rotation of the vertices before transforming their coordinates into screen position.

v2f vert (appdata v)
{
    v2f o;
    float3 rotVertex = rotation(v.vertex);
    o.vertex = UnityObjectToClipPos(rotVertex);
    o.uv = TRANSFORM_TEX(v.uv, _MainTex);
    return o;
}

In the exercise, a new three-dimensional vector called “rotVertex” has been declared. In it has been stored the input of mesh vertices and their rotation in object-space. This vector was then used as an argument in the UnityObjectToClipPos method.

If we go back to Unity and press the Play button, we will see the rotation of the Cube vertices as a whole.