《Unity着色器圣经》5.0.1 | 配置输入与输出

目录索引

译文

Chapter II | 光照，阴影与表面

在计算机图形学中，最复杂的概念之一是计算光照、阴影与表面。想要得到良好的视觉效果，必须执行一些函数或属性。在大多数情况下，这些函数或属性都非常专业，需要比较好的数学理解能力。

在正式开始学习光照、阴影与表面之前，让我们先详细介绍每个概念背后的理论，然后再介绍这些概念在 HLSL 语言中的实现。

值得一提的是，在 Unity 中已经有一些预定义好的程序（例如“标准表面着色器”、“光照 shader graph”），可以帮助我们进行模型表面的光照计算。但是作为初学者而言，我们有必要继续使用“无光照着色器（Unlit Shader）”类型的着色器学习，因为作为基本的颜色模型，它们允许我们实现自己的功能，更有助于我们理解如何在内置渲染管线（Built-in RP）或可编程渲染管线（SRP）中自定义光照及其相关概念。

5.0.1 | 配置输入与输出

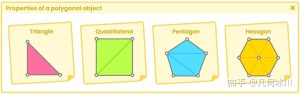
在第 3.3.0 小节中，我们学习了多边形物体的属性和语义之间的关系。同样，我们也可以看到后者是如何在结构体（struct）中初始化的。

在本小节中，我们将详细介绍如何配置模型的法线信息及其坐标空间从模型空间变换到世界空间的过程。

我们已经知道的是，如果我们需要使用模型的法线，就得把 NORMAL[n] 语义存储到一个三维向量中。第一步是在顶点输入中加入该值，如下面的代码所示：

struct appdata
{
   ...
    float3 normal : NORMAL;
};

向量的第四维对应于 W 分量，在正常情况下，法线的 W 分量默认值为 0，因为它是空间中的一个方向。

我们声明完顶点着色器输入中的法线之后，先问自己一个问题：我们需要把这些值传入片元着色器吗？如果回答“是”，我们还需要在顶点输出中再声明一遍法线。

这个例子同样适用于我们程序中使用的所有输入和输出。

struct v2f
{
   ...
    float3 normal : TEXCOORD1;
};

为什么我们需要同时在顶点输入和顶点输出中声明法线呢？因为我们不仅要连接属性与顶点着色器，还要将法线传入片元着色器。根据 HLSL 官方文档，片元着色器阶段并没有 NORMAL 语义，因此我们得用一个能够存储至少三维的向量的语义，这就是为什么我们在上面的代码中选择使用 TEXCOORD1。这个语义有四个维度（XYZW），是存储法线信息的理想载体。

在顶点输入与顶点输出中声明完属性之后，我们可以在顶点着色器中关联输入与输出：

v2f vert (appdata v) 
{ 
    v2f o; 
    … 
    // 我们将输入与输出关联起来
    o.normal = v.normal; 
    … 
    return o; 
}

刚刚这一步是什么意思？我们将顶点输出的结构体 v2f 中的法线与顶点输入的结构体 appdata 中的法线关联起来了。请记住，v2f 同时也是片元着色器的输入参数，这意味着我们可以将法线用在片元着色器阶段。

为了说明这一概念，让我们将创建一个名为 unity_light 的函数，并假设该函数负责在片段着色器阶段计算表面光照。这个函数本身并不执行任何实际操作，但它可以帮助我们学习：

void unity_light (in float3 normals, out float3 Out)
{
    Out = [Op] (normals);
}

根据该函数的声明，我们可以发现 unity_light 是一个具有两个输入参数（模型法线与输出值）的空函数。

请注意，所有的光照计算操作都需要将法线作为输入参数之一，因为如果没有法线信息，程序就无法知道光线应该如何与物体表面相互作用。

让我们在片元着色器中使用 unity_light 函数：

fixed4 frag (v2f i) : SV_Target 
{ 
    // 在向量中存储法线信息
    half3 normals = i.normal; 
    // 光照初始化为黑色
    half3 light = 0; 
    // 初始化函数，传入参数
    unity_light(normals, light); 

    return float4(light.rgb, 1); 
}

由于 unity_light 是一个空函数，因此创建了两个三维向量作为函数的参数。第一个参数代表法线，第二个则代表光照输出。

如果我们仔细观察，就会发现在上一阶段中声明的法线输出（i.normal）指的是模型空间中的法线。为什么这么说呢？因为到目前为止还没有进行任何类型的矩阵变换。

光照计算必须在世界空间中进行，因为入射光是在世界空间中的。同样的，场景中的物体的位置是根据网格中心确定的，因此我们必须在片元着色器阶段将法线的坐标空间变换到世界空间。

让我们进行以下步骤：

// 创建一个新的函数
half3 normalWorld (half3 normal) 
{ 
    return normalize(mul(unity_ObjectToWorld, float4(normal, 0))).xyz;
} 

half4 frag (v2f i) : SV_Target 
{ 
    // 将世界空间的法线存储在向量里
    float3 normals = normalWorld(i.normal); 
    float3 light = 0; 
    unity_light(normals, light); 
    return float4(light.rgb, 1); 
}

在上面的代码中，normalWorld 函数将法线坐标变换到了世界空间。在这个过程中，normalWorld 函数内使用了 unity_ObjectToWorld 矩阵，该矩阵允许我们从模型空间变换到世界空间。

空间变换中经常出现的一个问题是：为什么加上一个维度（W分量为0）的法线会出现在 normalWorld 函数中？

我们已经知道的是，法线指的是于空间中的一个“方向”，并不是一个“点”，这意味着它们的 W 分量必须等于 0。 unity_ObjectToWorld 是一个 4 * 4 的矩阵，因此我们将在 XYZW 通道（四维）中获得法线的新方向。

因此，我们必须确保给 W 分量赋值为“0”（float4(normal. xyz, 0)）。根据算术法则，任何数字乘以 0 都等于 0，这样就可以准确无误地计算出法线。

上述坐标空间转换的过程也可以在顶点着色器阶段进行，操作方法基本相同。但如果我们在顶点着色器中进行该操作的话可以优化程序，因为法线是按顶点而不是按像素计算的。

v2f vert (appdata v)
{
   ...
    o.normal = normalize(mul(unity_ObjectToWorld, float4(v.normal, 0))).xyz;
   ...
}

---

原文对照

Chapter II | Lighting, shadows and surfaces

One of the most complex concepts in computer graphics is the calculation of lighting, shadows, and surfaces. The operations we must perform to obtain good results depend on several functions and/or properties, that in most cases, are very technical and require a high level of mathematical understanding.

Before starting to create our functions for lighting, shadow, and surface calculations, we begin by detailing the theory behind each concept and then move on to their implementation in the HLSL language.

It is worth mentioning that in Unity we have some predefined programs that facilitate lighting calculations for a surface (e.g. Standard Surface, Lit Shader Graph) however, it is essential to continue our study using Unlit Shader type Shaders, since being basic color models, they allow us to implement our own functions, and thus, obtain the necessary understanding generating customized lighting and its derivatives, either in Built-in RP or Scriptable RP.

5.0.1 | 配置输入与输出

In section 3.3.0 of the previous chapter, we learned the analogy between the property of a polygonal object and a semantic. Likewise, we could see how the latter is initialized within a struct.

In this section, we will detail the steps necessary to configure the normals of our object and transform its coordinates from object-space to world-space.

As we already know, if we want to work with our object normals then we have to store the semantic NORMAL[n] in a three-dimensional vector. The first step is to include this value in the vertex input, as shown in the following example.

struct appdata
{
   ...
    float3 normal : NORMAL;
};

Remember that the fourth dimension of a vector corresponds to its W component, which, in the normal case, has a “zero” default value since it is a direction in space.

Once we have declared our object normals as input, we must ask the following question: are we going to need to pass these values to the fragment shader stage? If the answer is yes, then we will have to declare the normals once again, but this time as output.

This analogy applies equally to all the inputs and outputs that we use in our program.

struct v2f
{
   ...
    float3 normal : TEXCOORD1;
};

Why have we declared normals in both vertex input and vertex output? This is because we will have to connect both properties within the vertex shader stage, and then pass them to the fragment shader stage. It should be noted that, according to the official HLSL documentation, there is no NORMAL semantic for the fragment shader stage, therefore, we must use a semantic that can store at least three coordinates of space. That is why we have used TEXCOORD1 in the example above. This semantic has four dimensions (XYZW) and is ideal for working with normals.

After having declared a property in both vertex input and vertex output, we can go to the vertex shader stage to connect them.

v2f vert (appdata v) 
{ 
    v2f o; 
    … 
    // we connect the output with the input 
    o.normal = v.normal; 
    … 
    return o; 
}

What did we just do? Basically, we connected the normals output of struct v2f with the normals input of struct appdata. Remember that v2f is used as an argument in the fragment shader stage, this means that we can use the object normals as a property in this stage.

To illustrate this concept we will create an example function, which we will call unity_light and will be responsible for calculating the lighting on a surface in the fragment shader stage.

In itself, this function is not going to perform any actual operation; however, it will help us to understand some factors that we should know.

void unity_light (in float3 normals, out float3 Out)
{
    Out = [Op] (normals);
}

According to its declaration, we can observe that unity_light is an empty function; that has two arguments: The object normals and the output value.

Note that all lighting calculation operations require the normal as one of their variables, why? Because without this, the program will not know how light should interact with the object surface.

We will apply the unity_light function in the fragment shader stage.

fixed4 frag (v2f i) : SV_Target 
{ 
    // store the normals in a vector 
    half3 normals = i.normal; 
    // initialize our light in black 
    half3 light = 0; 
    // initialize our function and pass the vectors 
    unity_light(normals, light); 

    return float4(light.rgb, 1); 
}

Since unity_light corresponds to an empty function, two three-dimensional vectors have been created which will be used as arguments in the function.

The first one corresponds to the normals, and the second, the output value, to the lighting output.

If we look closely, we will notice that the normals output that was declared in the previous stage (i.normal) is in object-space, how do we know this? We can easily determine this because there has not been any type of matrix transformation generated up to this point.

The operations for the lighting calculation must be in world-space, why? Because incidence values are found in the world; within a scene, likewise, the objects have a position according to the center of a grid, therefore, we will have to transform the space coordinates of the normals in the fragment shader stage.

To do this, we do the following:

// let's create a new function 
half3 normalWorld (half3 normal) 
{ 
    return normalize(mul(unity_ObjectToWorld, float4(normal, 0))).xyz;
} 

half4 frag (v2f i) : SV_Target 
{ 
    // store the world-space normals in a vector 
    float3 normals = normalWorld(i.normal); 
    float3 light = 0; 
    unity_light(normals, light); 
    return float4(light.rgb, 1); 
}

In the example above, the normalWorld function returns the space coordinates transformation to the normals. In its process, it uses the unity_ObjectToWorld matrix, which allows us to go from object-space to world-space.

A question that frequently arises in the transformation of spaces is, why are the normals within a four-dimensional vector in the normalWorld multiplication function?

As we already know the normals correspond to a direction in space, this means that their W component must equal “zero”. unity_ObjectToWorld is a four-by-four-dimensional matrix, as a result, we will obtain a new direction for the normals in their four XYZW channels.

Therefore, we must make sure to assign the value “zero” to the W component (float4(normal. xyz, 0)), because, by arithmetic rules, any number multiplied by zero equals zero, and thus, the normals can be calculated without errors.

The process mentioned above can also be carried out in the vertex shader stage. The operation is basically the same, except that if we do it at this stage, there will be a degree of optimization because the normals will be calculated by vertices and not by the number of pixels on the screen.

v2f vert (appdata v)
{
   ...
    o.normal = normalize(mul(unity_ObjectToWorld, float4(v.normal, 0))).xyz;
   ...
}