《Unity着色器圣经》7.0.3 | 漫反射

目录索引

译文

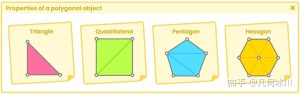
一般来说，物体表面有两种类型的反射：漫反射和镜面反射。漫反射（Diffuse Reflection）遵循约翰·海因里希·兰伯特（Johann Heinrich Lambert）的兰伯特余弦辐射体，兰伯特在考虑光源方向和物体表面法线的前提下模拟了物体表面和光源之间的关系。

在 Maya 3D 中，我们可以找到一个名为“Lambert（兰伯特）”的材质，默认添加了漫反射。在 Blender 中也有一个漫反射材质，只不过这个材质的名字是“Diffuse（漫反射）”。两个材质执行的操作相同，结果也非常相似，只是渲染管线架构因软件而异。

根据约翰·海因里希·兰伯特 的研究，通过下面的公式就可以得到完美的漫反射效果：

D = Dᵣ Dₗ max(0, n · l)

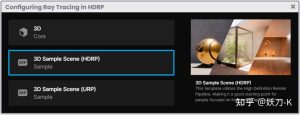
这个公式要怎么用着色器代码表示呢？在开始编程之前，我们先了解一下光和物体表面之间的关系。假设我们现在有一个球体和一束平行光：

在上面的例子中，漫反射通过模型表面的法线 normal [n] 和光源的方向 direction [l] 之间的夹角（通过两个向量点乘得出）计算得出。然而，考虑到光线反射的性质，还需要考虑其他计算，比如 [Dr] 和 [Dl]，它们分别对应于光源反射颜色（reflection color）和光源强度（intensity）的反射量。因此，上述等式可转换如下：

漫反射 [D] 等于光源反射颜色 [Dr] 与光源强度 [Dl] 的乘积，再乘以零 [0] 与表面法线和照明方向之间的点乘结果 [n · l] 之间的最大值。

为了更好地理解这个概念，让我们创建一个名为 USB_diffuse_shading 的无光照着色器。在着色器中，让我们创建一个名为“LambertShading”的函数，并包含前文提到的属性。

Shader "USB/USB_diffuse_shading"
{
    Properties { ... }
    SubShader
    {
        Pass
        {
            CGPROGRAM
            ...
            float3 LambertShading() { ... }
            ...
            ENDCG
        }
    }
}

// internal structure of the LambertShading function 
float3 LambertShading 
( 
    float3 colorRefl, // Dr，光源反射颜色
    float lightInt, // Dl，光源强度
    float3 normal, // n，法线
    float3 lightDir // l，光源方向
) 
{ 
    return colorRefl* lightInt * max(0, dot(normal, lightDir)); 
}

LambertShading 函数返回了一个的三维向量，用来表示颜色。函数的输入参数有光源反射颜色（colorRefl RGB）、光源强度（lightInt [0, 1]）、模型表面法线（normal XYZ）和光源方向（lightDir XYZ）。

值得注意的是，这里输入的法线和光源方向都应该是世界空间下的，因此我们需要先在顶点着色器阶段进行变换。

我们无需变换光源，因为可以使用 Unity 内部变量 _WorldSpaceLightPos0 ，它指的是世界空间中的光照方向。

因为光源强度的范围在 [0.0f, 1.0f] 之间，我们可以通过在属性中声明一个浮点数范围 _LightInt 来表示它：

Shader "USB/USB_diffuse_shading"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _LightInt ("Light Intensity", Range(0, 1)) = 1
    }
    SubShader { ... }
}

我们通过 _LightInt 来控制 LambertShading 函数中光照强度的变化。作为着色器程序的一部分，我们也需要为其声明连接变量：

Pass
{
    CGPROGRAM
    ...
    sampler2D _MainTex;
    float4 _MainTex_ST;
    float _LightInt;
    ...
    ENDCG
}

现在我们的属性和连接变量都声明好了，我们需要在片元着色器中使用 LambertShading 函数。让我们声明一个名为“diffuse”的新三维向量，让它与 LamberShading 函数相等，以获取函数的返回值：

float3 LambertShading() { … } 

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 
    // LambertShading(1, 2, 3, 4); 
    half3 diffuse = LambertShading( 0, _LightInt, 0, 0); 

    return col; 
}

我们已经知道，LambertShading 函数有四个输入参数，分别是：

• colorRefl.
• lightInt.
• normal.
• lightDir.

在上面的例子中，除了光照强度“lightInt”被设成属性 _LightInt 之外，其他参数目前都被设成了 0 。

现在让我们看看反射光颜色这个参数，我们可以使用 Unity 内置变量 _LightColor[n] 来获取场景中的光源颜色。我们可以按照下面代码中的写法在 CGPROGRAM 中使用该内置变量：

Pass
{
    CGPROGRAM
    ...
    sampler2D _MainTex;
    float4 _MainTex_ST;
    float _LightInt;
    float4 _LightColor0;
    ...
    ENDCG
}

现在，我们将其用作 LambertShading 函数中的第一个参数了，让我们再声明一个新的三维向量 colorRelf 来获取光源反射颜色的 RGB 通道的值。

fixed4 frag (v2f i) : SV_Target
{
    fixed4 col = tex2D(_MainTex, i.uv);
    fixed3 colorRefl = _LightColor0.rgb;
    half3 diffuse = LambertShading( colorRefl, _LightInt, 0, 0);

    return col;
}

对于光照方向，我们可以使用 Unity 内置变量 _WorldSpaceLightPos[n] 来获取，它表示了世界空间中光源的光照方向。

和 _LightColor[n] 不同的是，没有必要将其声明为全局变量，因为它已经包含在 #include “UnityCG.cginc” 里了，我们可以直接把它作为函数的参数使用：

fixed4 frag (v2f i) : SV_Target
{
    fixed4 col = tex2D(_MainTex, i.uv);
    float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);
    fixed3 colorRefl = _LightColor0.rgb;
    half3 diffuse = LambertShading( colorRefl, _LightInt, 0, lightDir);

    return col;
}

在上面的例子中，我们声明了一个三维向量 lightDir，用来存储光照方向的 XYZ 通道的值。另外，由于我们使用了归一化函数（normalize），因此 lightDir 的大小为 [1] 。最后，将光照方向作为第四个参数传入函数中。

现在四个输入参数只差世界空间下的模型法线了。让我们来到顶点输入与顶点输出两个结构体，在其中加入相应的语义：

CGPROGRAM 
… 
// 顶点输入
struct appdata 
{ 
    float4 vertex : POSITION; 
    float2 UV : TEXCOORD0; 
    float3 normal : NORMAL; 
}; 

// 顶点输出
struct v2f 
{ 
    float2 UV : TEXCOORD0; 
    float4 vertex : SV_POSITION; 
    float3 normal_world : TEXCOORD1; 
}; 
… 
ENDCG

请记住，我们之所以同时在顶点输入与输出中配置法线，是因为我们需要在片元着色器阶段中的 LambertShading 中使用它，而法线的变换是在顶点着色器阶段完成的，因此需要在顶点着色器中关联起来：

v2f vert (appdata v)
{
    v2f o;
    o.vertex = UnityObjectToClipPos(v.vertex);
    o.uv = TRANSFORM_TEX(v.uv, _MainTex);
    o.normal_world = normalize(mul(unity_ObjectToWorld, float4(v.normal, 0))).xyz;

    return o;
}

unity_ObjectToWorld 矩阵与模型法线之间乘积的归一化结果被存储在了 normal_world 向量中。这意味着 normal_world 中的法线是位于世界空间中的，并且大小为 [1] 。

现在来到片元着色器阶段，声明一个新的三维向量 normal 用于存储来自顶点输出的世界空间法线，并将其传入 LambertShading 函数中，

fixed4 frag (v2f i) : SV_Target
{
    fixed4 col = tex2D(_MainTex, i.uv);
    
    float3 normal = i.normal_world;
    float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);
    fixed3 colorRefl = _LightColor0.rgb;
    half3 diffuse = LambertShading(colorRefl, _LightInt, normal, lightDir);
    
    return col;
}

接着，将漫反射结果 diffuse 与纹理的 RGB 颜色相乘。因为我们希望着色器能受到光源的影响，因此我们需要在程序中包含 LightMode ForwardBase，从而配置渲染路径。

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    float3 normal = i.normal_world; 
    float3 lightDir = normalize(_WorldSpaceLightPos0.xyz); 
    fixed3 colorRefl= _LightColor0.rgb; 
    half3 diffuse = LambertShading(colorRefl, _LightInt, normal, lightDir); 

    // 漫反射作用于纹理
    col.rgb *= diffuse; 

    return col; 
}

为了完成刚才提到的操作，现在来到子着色器下的标签（Tags）语义块，配置渲染路径：

SubShader
{
    Tags { "RenderType"="Opaque" }
    Pass
    {
        Tags { "LightMode"="ForwardBase" }
    }
}

---

原文对照

Generally, a surface can be defined by two types of reflection: “matte or gloss”. Diffuse reflection obeys Johann Heinrich Lambert’s Lambert’s cosine law, he makes an analogy between illumination and the surface of an object, considering the light source direction and the surface normal.

In Maya 3D we can find a material called Lambert which adds diffuse reflection by default. This same concept is applied in Blender, with the difference that the material is called Diffuse, however, the same operation is performed in both cases and the result is quite similar, with render pipeline architecture variations according to each software.

According to Johann Heinrich Lambert, we must carry out the following operation to obtain a perfect diffusion:

D = Dᵣ Dₗ max(0, n · l)

How does this equation translate into code? To answer this question, we must first understand the analogy between the illumination and the normal direction of a surface. Let’s assume that we have a Sphere and a directional light pointing towards it as follows:

In the example above, the diffusion is calculated according to the angle between the normal [n] of the surface and the lighting direction [l], which in fact, corresponds to the dot product between these two properties. However, there are other calculations to consider given the nature of reflection, these refer to [D r ] and [Dl ] which correspond to the amount of reflection in terms of color and intensity. Consequently, the above equation can be translated as follows:

Diffusion [D] equals the multiplication of the reflection color of the light source [Dr ] and its intensity [Dl ], and the maximum (max) between zero [0] and the result of the product point between the surface normal and the lighting direction [n · l].

To understand this definition better, we will create a new Unlit Shader, which we will call USB_diffuse_shading. We start by creating a function, calling it “LambertShading” and include the properties mentioned above, so it operates correctly.

Shader "USB/USB_diffuse_shading"
{
    Properties { ... }
    SubShader
    {
        Pass
        {
            CGPROGRAM
            ...
            float3 LambertShading() { ... }
            ...
            ENDCG
        }
    }
}

// internal structure of the LambertShading function 
float3 LambertShading 
( 
    float3 colorRefl, // Dr 
    float lightInt, // Dl 
    float3 normal, // n 
    float3 lightDir // l 
) 
{ 
    return colorRefl* lightInt * max(0, dot(normal, lightDir)); 
}

The LambertShading function returns a three-dimensional vector for its RGB colors. As an argument we have used the light reflection color (colorReflRGB), the light intensity (lightInt [0, 1]), the surface normals (normal XYZ), and the lighting direction (lightDir XYZ).

It is worth pointing out that, both the normals and the lighting direction will be calculated in world-space, therefore, we will have to transform the normals in the vertex shader stage.

For lighting, it is not necessary to generate a transformation because we can use the internal variable _WorldSpaceLightPos0 which refers to the direction of directional light in world-space, included by default in Unity.

Because the intensity of light can be zero or one [0.0f, 1.0f], we can start its implementation by going to the properties to declare a floating variable. In the next exercise, we will generate a floating type property, which we will call _LightInt. This will be responsible for controlling the light intensity between the aforementioned range.

Shader "USB/USB_diffuse_shading"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _LightInt ("Light Intensity", Range(0, 1)) = 1
    }
    SubShader { ... }
}

We use _LightInt to increase or decrease light intensity in our LambertShading function. As part of the process, we must then declare an internal variable to generate the connection between the property and our program.

Pass
{
    CGPROGRAM
    ...
    sampler2D _MainTex;
    float4 _MainTex_ST;
    float _LightInt;
    ...
    ENDCG
}

Now our property is set up, we must implement the LambertShading function in the fragment shader stage. To do this, we will go to the stage and declare a new three-dimensional vector, we will call it “diffuse” and make it equal to the LambertShading function.

float3 LambertShading() { … } 

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 
    // LambertShading(1, 2, 3, 4); 
    half3 diffuse = LambertShading( 0, _LightInt, 0, 0); 

    return col; 
}

As we already know, the LambertShading function has four arguments, which are:

• colorRefl.
• lightInt.
• normal.
• lightDir.

In the example above, we have initialized these arguments to “zero” except for “lightInt” which, given its nature, must be replaced by the property _LightInt in the second box.

We will continue with the reflection color, for this, we can use the internal variable _LightColor[n], which refers to the lighting color in our scene. To use it, we must first declare it as a uniform variable within the CGPROGRAM as follows:

Pass
{
    CGPROGRAM
    ...
    sampler2D _MainTex;
    float4 _MainTex_ST;
    float _LightInt;
    float4 _LightColor0;
    ...
    ENDCG
}

Now we can use it as the first argument in the LambertShading function and declare a new three-dimensional vector using only the light’s RGB colors.

fixed4 frag (v2f i) : SV_Target
{
    fixed4 col = tex2D(_MainTex, i.uv);
    fixed3 colorRefl = _LightColor0.rgb;
    half3 diffuse = LambertShading( colorRefl, _LightInt, 0, 0);

    return col;
}

For the lighting direction, we can use the internal variable _WorldSpaceLightPos[n], which, as we already mentioned, refers to the direction of directional light in world-space.

Unlike _LightColor[n], it is not necessary to declare this variable as a uniform vector because it has already been initialized in the #include “UnityCG.cginc”, so we can use it directly as an argument in our function.

fixed4 frag (v2f i) : SV_Target
{
    fixed4 col = tex2D(_MainTex, i.uv);
    float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);
    fixed3 colorRefl = _LightColor0.rgb;
    half3 diffuse = LambertShading( colorRefl, _LightInt, 0, lightDir);

    return col;
}

In the example above, a three-dimensional vector has been declared to save the lighting direction values in its XYZ coordinates. In addition, the function has been normalized so that the resulting vector has a magnitude of “one” [1]. Finally, the lighting direction has been positioned as the fourth argument in the function.

Only the third argument that corresponds to the world-space object normals is missing, for this we have to go to both the vertex input and the vertex output and include this semantic.

CGPROGRAM 
… 
// vertex input 
struct appdata 
{ 
    float4 vertex : POSITION; 
    float2 UV : TEXCOORD0; 
    float3 normal : NORMAL; 
}; 

// vertex output 
struct v2f 
{ 
    float2 UV : TEXCOORD0; 
    float4 vertex : SV_POSITION; 
    float3 normal_world : TEXCOORD1; 
}; 
… 
ENDCG

Remember that the reason why we are configuring the normals in both the vertex input and output is precisely because we will use them in the fragment shader stage, where our LambertShading function has been initialized, however, their connection will be made in the vertex shader stage to optimize the transformation process.

v2f vert (appdata v)
{
    v2f o;
    o.vertex = UnityObjectToClipPos(v.vertex);
    o.uv = TRANSFORM_TEX(v.uv, _MainTex);
    o.normal_world = normalize(mul(unity_ObjectToWorld, float4(v.normal, 0))).xyz;

    return o;
}

The normalized factor between the unity_ObjectToWorld matrix and the object normal input has been stored in the vector normal_world. This means that the normals have been configured in world-space and have a magnitude of “one” [1].

Now we can go to the fragment shader stage, declare a new three-dimensional vector, and pass the normal output as the third argument in the LambertShading function.

fixed4 frag (v2f i) : SV_Target
{
    fixed4 col = tex2D(_MainTex, i.uv);
    
    float3 normal = i.normal_world;
    float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);
    fixed3 colorRefl = _LightColor0.rgb;
    half3 diffuse = LambertShading(colorRefl, _LightInt, normal, lightDir);
    
    return col;
}

In the above example, we declare a three-dimensional vector called normal, to which we pass the object normals. Then, we use this vector as the third argument in the LambertShading function.

Next, multiply the diffusion by the texture’s RGB color and, since our shader is interacting with a light source, we will need to include the LightMode ForwardBase, thus the render path will be configured.

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    float3 normal = i.normal_world; 
    float3 lightDir = normalize(_WorldSpaceLightPos0.xyz); 
    fixed3 colorRefl= _LightColor0.rgb; 
    half3 diffuse = LambertShading(colorRefl, _LightInt, normal, lightDir); 
    // diffuse is included in the texture 
    col.rgb *= diffuse; 

    return col; 
}

To finish, go to the Tags and configure the render path.

SubShader
{
    Tags { "RenderType"="Opaque" }
    Pass
    {
        Tags { "LightMode"="ForwardBase" }
    }
}