《Unity着色器圣经》7.0.6 | 菲涅尔效应

目录索引

译文

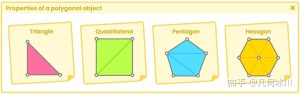
菲涅尔（Fresnel）效应（由奥古斯丁-让·菲涅耳发现）也被称为边缘效应（Rim effect），是一种反射，其大小与物体法线与相机方向的夹角成正比。

模型表面距离相机越远，菲涅尔反射就越多，因为入射方向（相机）与物体法线之间的角度越大。

当入射方向（相机）与法线之间的夹角为“0°”时没有反射存在，因为两个向量是平行的。当入射方向与法线之间的夹角为“90°”时全反射，两个向量相互垂直。这非常有趣，因为当没有反射时函数返回黑色，全反射时则返回白色，这些值对应于像素的最大和最小光照值。

为了理解这个概念，我们需要分析来自 Shader Graph 中的 Fresnel Effect 节点函数。

void unity_FresnelEffect_float(
    in float3 normal,
    in float3 viewDir,
    in float power,
    out float Out
)
{
    Out = pow((1 - saturate(dot(normal, viewDir))), power);
}

在这个函数中发生了一些事情，我们将在本节中进行详细介绍，现在我们暂时先只关注输出的内部操作。这一操作可分为三个过程：

saturate(dot(normal, viewDir))

这个操作将确定入射方向与模型法线之间的夹角，并返回范围在 0 ~ 1（[0.0f, 1.0f]）之间的数。

我们已经知道，“点乘（dot）”函数根据夹角的值将返回计算结果。由于反射操作只需要一个介于“0”和“1”之间的值，因此我们添加了函数 saturate，以限制这个范围之间的值。

// 最小返回“0”，最大返回“1”
float saturate (float x) 
{ 
    return max(0, min(1, x)); 
} 

// 允许设置最小值与最大值的区间
float clamp (float x, float a, float b) 
{ 
    return max(a, min(b, x)); 
}

Saturate 函数与 clamp 函数功能类似，不同之处在于后者可以修改最小值和最大值来控制范围。

让我们从“1 – x”继续。

( 1 – x )

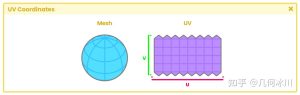
要理解这个操作的本质，我们必须回到之前的练习。当视线方向和表面法线平行且指向同一方向时，点乘将返回 “1”。这对我们来说是个问题，因为我们需要该操作返回“0”，也就是黑色。

而“1 – x”运算具有如下翻转结果的功能：

// 如果法线和视线方向在同一方向上平行 
saturare(dot(float3(0, 1, 0), float3(0, 1, 0))) = 1 
1 - 1 = 0 

// 如果法线和视线方向垂直 
saturare(dot(float3(0, 1, 0), float3(1, 0, 0))) = 0 
1 - 0 = 1 

最后，在函数中，我们可以找到“pow(x, power)”运算。该运算允许我们增加或减少反射的范围。

让我们创建一个名为 USB_fresnel_effect 的无光照着色器帮助我们更好的了解 Shader Graph 中的 Fresnel 节点中的操作。让我们在着色器中加入以下代码：

Shader "USB/USB_fresnel_effect"
{
    Properties { ... }
    SubShader
    {
        Pass
        {
            CGPROGRAM
            ...
            void unity_FresnelEffect_float() { ... }
            ...
            ENDCG
        }
    }
}

需要注意的是，函数 unity_FresnelEffect_float 的返回类型是“void”，在第 4.0.4 小节中我们曾学习了无返回值和有返回值的函数的区别。在上述的代码中，我们声明了一些变量，并将它们作为参数传入函数中。

让我们在片元着色器中声明该函数。

void unity_FresnelEffect_float() { … } 

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    // 初始化无返回值函数
    unity_FresnelEffect_float(0, 0, 0, 0); 

    return col; 
}

函数的第一个参数代表了物体在世界空间的法线，所以我们需要在顶点输入的结构体中使用 NORMAL 语义，并在顶点着色器阶段变换法线的坐标空间。

由于我们需要在片元着色器中使用法线，因此需要在顶点输出结构体中声明一个向量用以存储变换后的法线。

// 顶点输入
struct appdata 
{ 
    float4 vertex : POSITION; 
    float2 uv : TEXCOORD0; 
    float3 normal : NORMAL; 
};

// 顶点输出
struct v2f 
{ 
    float4 vertex : SV_POSITION; 
    float2 uv : TEXCOORD0; 
    float3 normal_world : TEXCOORD1; 
    float3 vertex_world : TEXCOORD2; 
};

顶点输出结构体中的向量 vertex_world 用于计算视线方向。

如果我们多加留心，就会发现上面的步骤和前面学习反射的小节中所演示的代码一致。

v2f vert (appdata v)
{
    v2f o;
    o.vertex = UnityObjectToClipPos(v.vertex);
    o.uv = TRANSFORM_TEX(v.uv, _MainTex);
    o.normal_world = normalize(mul(unity_ObjectToWorld, float4(v.normal, 0))).xyz;
    o.vertex_world = mul(unity_ObjectToWorld, v.vertex);
    return o;
}

现在让我们来到片元着色器中声明两个向量，一个代表法线、另一个代表视线方向。

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    float3 normal = i.normal_world; 
    float3 viewDir = normalize(_WorldSpaceCameraPos - i.vertex_world); 

    // 将法线与视线方向传入函数中
    unity_FresnelEffect_float(normal, viewDir, 0, 0); 

    return col; 
}

在上面的例子中，三维向量 normal 已经存储了世界空间的法线值；另一个三维向量 viewDir 则计算了视线方向，两个向量均作为参数传入 unity_FresnelEffect_float 函数中，并将在函数内的计算中被使用。第三个参数是“菲涅尔指数”，我们可以传入一个范围来控制反射的范围。

Shader "USB/USB_fresnel_effect"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _FresnelPow ("Fresnel Power", Range(1, 5)) = 1
        _FresnelInt ("Fresnel Intensity", Range(0, 1)) = 1
    }
    SubShader { ... }
}

我们将 _FresnelPow 属性作为函数的第三个参数。作为一个指数值，我们将使用 _FresnelInt 属性来增加或减少对象中的菲涅尔效应的量。接着，我们需要在程序中为这两个属性声明连接变量：

CGPROGRAM
...
sampler2D _MainTex;
float4 _MainTex_ST;
float _FresnelPow;
float _FresnelInt;
...
ENDCG

这一步完成之后，属性与后续的着色器程序产生关联，我们就可以在 Unity 的检查其中动态修改它们了。现在，我们将 _FresnelPow 作为第三个参数传入函数中。

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    float3 normal = i.normal_world; 
    float3 viewDir = normalize(_WorldSpaceCameraPos - i.vertex_world); 

    // 将指数值传入函数中 
    unity_FresnelEffect_float(normal, viewDir, _FresnelPow, 0); 

    return col; 
}

第四个参数对应的是函数输出值，我们将在这里保存颜色输出。为此，我们只需在函数中创建并添加一个浮点数类型的变量：

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    float3 normal = i.normal_world; 
    float3 viewDir = normalize(_WorldSpaceCameraPos - i.vertex_world); 
    // initialize the color output in black 
    float fresnel = 0; 

    // 添加输出颜色
    unity_FresnelEffect_float(normal, viewDir, _FresnelPow, fresnel); 

    col += fresnel * _FresnelInt; 
    return col; 
}

在上面的例子中，我们声明了一个名为 fresnel 的变量并赋值为“0”（黑色），它作为第四个参数被传入函数中并作为其输出值，即 unity_ FresnelEffect_float 函数的最终运算结果。

完成编写后，我们就可以看到菲涅尔反射的效果了。由于其强度（_FresnelInt）已被添加到名为“col”的基本纹理颜色中，这样就为场景中的物体增加了反射效果，同时也允许我们修改其强度值。

---

原文对照

The Fresnel effect (after its creator Augustin Jean Fresnel), also known as the Rim effect, is a type of reflection where its size is proportional to the incidence angle; the angle between the object normals and the camera direction.

The further the surface is from the camera, the more Fresnel reflection there will be because the angle between the incidence value and the object normals is greater.

When the angle between the incidence value and the normals equals “zero” degrees there is no reflection, because both vectors are parallel, on the other hand, when the angle equals “ninety” degrees, the reflection is full, and the vectors are perpendicular. This is quite interesting because, when the reflection is null, our program must return black. On the contrary, when it is full, it returns white, why? Because these correspond to the maximum and minimum illumination values of a pixel.

To understand this concept, we must analyze the following function coming from the Fresnel Effect node in the Shader Graph.

void unity_FresnelEffect_float(
    in float3 normal,
    in float3 viewDir,
    in float power,
    out float Out
)
{
    Out = pow((1 - saturate(dot(normal, viewDir))), power);
}

In the previous function several things are happening that we will detail throughout this section, for now, we will only focus on the output’s internal operation. This operation can be divided into three processes:

saturate(dot(normal, viewDir))

This operation determines the angle between the incidence vector and the object normals, and as a result, returns a numerical range between “zero and one” [0.0f, 1.0f].

As we already know, the “dot” function will return “one, zero or minus one” depending on the angle between its arguments [-1.0f, 1.0f]. Since the reflection operation requires only a value between “zero and one,” the intrinsic function saturate has been added, limiting the values between this range.

// it only can return "0" as minimum and "1" as maximum 
float saturate (float x) 
{ 
    return max(0, min(1, x)); 
} 

// it can modify the minimum and maximum range 
float clamp (float x, float a, float b) 
{ 
    return max(a, min(b, x)); 
}

Saturate fulfills the same function as clamp, with the difference that with the latter we can modify the minimum and maximum value to generate the limit.

Let’s continue with the operation “1 – x”.

( 1 – x )

To understand its nature, we must return to the previous exercise. Dot product will return “one” [1] when the view direction vector and the normals are parallel and point in the same direction. This is a problem for us, because we need the operation to return “zero” [0] which is equivalent to black.

The operation “1 – x” has the function of flipping the result as follows.

// if the normals and the view are parallel in the same direction 
saturare(dot(float3(0, 1, 0), float3(0, 1, 0))) = 1 
1 - 1 = 0 

// if the normals and the view are perpendicular 
saturare(dot(float3(0, 1, 0), float3(1, 0, 0))) = 0 
1 - 0 = 1 

Finally, in the function, we can find the operation “pow( x,power )” which allows us to increase or decrease the range of reflection.

To understand in detail the Fresnel operation of Shader Graph, we will start a new Unlit Shader that we will call USB_fresnel_effect. The first thing we must do is to include this function within our program.

Shader "USB/USB_fresnel_effect"
{
    Properties { ... }
    SubShader
    {
        Pass
        {
            CGPROGRAM
            ...
            void unity_FresnelEffect_float() { ... }
            ...
            ENDCG
        }
    }
}

It should be noted that the function unity_FresnelEffect_float is a “void” type. In section 4.0.4 of Chapter I, we reviewed the difference between implementing an empty function and one that returns a value. In this case, we have to declare some variables and pass them as arguments, as appropriate.

We will start by declaring the function in the fragment shader stage.

void unity_FresnelEffect_float() { … } 

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 
    // initialize the void function 
    unity_FresnelEffect_float(0, 0, 0, 0); 

    return col; 
}

The first argument in the function corresponds to the object normals in world-space, so we have to go to vertex input and use NORMAL semantics, and then transform its space coordinates in the vertex shader stage.

Due to the fact that we use the normals in the fragment shader stage, we have to declare a vector in the vertex output, this way we can store the result of the transformation.

// vertex input 
struct appdata 
{ 
    float4 vertex : POSITION; 
    float2 uv : TEXCOORD0; 
    float3 normal : NORMAL; 
};

// vertex output 
struct v2f 
{ 
    float4 vertex : SV_POSITION; 
    float2 uv : TEXCOORD0; 
    float3 normal_world : TEXCOORD1; 
    float3 vertex_world : TEXCOORD2; 
};

The vector vertex_world has been added to the vertex output because we need this variable to calculate the view direction.

If we pay attention, we will notice that the process is exactly the same as we have done in previous sections for the reflection calculation.

v2f vert (appdata v)
{
    v2f o;
    o.vertex = UnityObjectToClipPos(v.vertex);
    o.uv = TRANSFORM_TEX(v.uv, _MainTex);
    o.normal_world = normalize(mul(unity_ObjectToWorld, float4(v.normal, 0))).xyz;
    o.vertex_world = mul(unity_ObjectToWorld, v.vertex);
    return o;
}

To continue with the implementation of the Fresnel function, we will return to the fragment shader stage and declare two vectors: one for the normals calculation and the other for the view direction.

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    float3 normal = i.normal_world; 
    float3 viewDir = normalize(_WorldSpaceCameraPos - i.vertex_world); 
    // assign the normals and view direction to the function 
    unity_FresnelEffect_float(normal, viewDir, 0, 0); 

    return col; 
}

In the example above, a three-dimensional vector called normal has been declared to store the normals output value in world-space. Then a new vector called viewDir has been declared which contains the view direction calculation. Both vectors have been assigned as the first and second arguments in the function unity_FresnelEffect_float, since they are required in its internal operation. For the third argument (fresnel power) we have to declare a property with a numerical range. This will be used to modify the reflection range.

Shader "USB/USB_fresnel_effect"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _FresnelPow ("Fresnel Power", Range(1, 5)) = 1
        _FresnelInt ("Fresnel Intensity", Range(0, 1)) = 1
    }
    SubShader { ... }
}

We will use the property _FresnelPow as a third argument in the function, as an exponential value; while we will use _FresnelInt to increase or decrease the amount of Fresnel effect in the object. As we already know, we must declare connection variables for both properties within our program.

CGPROGRAM
...
sampler2D _MainTex;
float4 _MainTex_ST;
float _FresnelPow;
float _FresnelInt;
...
ENDCG

Once this process is done, the property will be connected to our program, this means that we can dynamically modify the reflection range from the Unity Inspector. Now we can use _FresnelPow as the third argument in the function.

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    float3 normal = i.normal_world; 
    float3 viewDir = normalize(_WorldSpaceCameraPos - i.vertex_world); 
    // add the exponent value in the function 
    unity_FresnelEffect_float(normal, viewDir, _FresnelPow, 0); 

    return col; 
}

The fourth corresponds to the function output value, where we will save the color output. To do this, we simply create and add a floating variable to the function.

fixed4 frag (v2f i) : SV_Target 
{ 
    fixed4 col = tex2D(_MainTex, i.uv); 

    float3 normal = i.normal_world; 
    float3 viewDir = normalize(_WorldSpaceCameraPos - i.vertex_world); 
    // initialize the color output in black 
    float fresnel = 0; 
    // add the output color 
    unity_FresnelEffect_float(normal, viewDir, _FresnelPow, fresnel); 

    col += fresnel * _FresnelInt; 
    return col; 
}

In the previous example, a variable called fresnel was declared, which was initialized at “zero” (black). It was then included in the function as the fourth argument, as output. This means that within this variable is the result of the final operation that occurs in the unity_ FresnelEffect_float function.

At the end of the operation, we can see that the fresnel variable result, due to its intensity (_FresnelInt), was added to the base texture color called “col”. This adds reflection to the object in our scene and also allows us to modify its intensity value.